1870. Minimum Speed to Arrive on Time

We can visaulize the problem with the following graph:

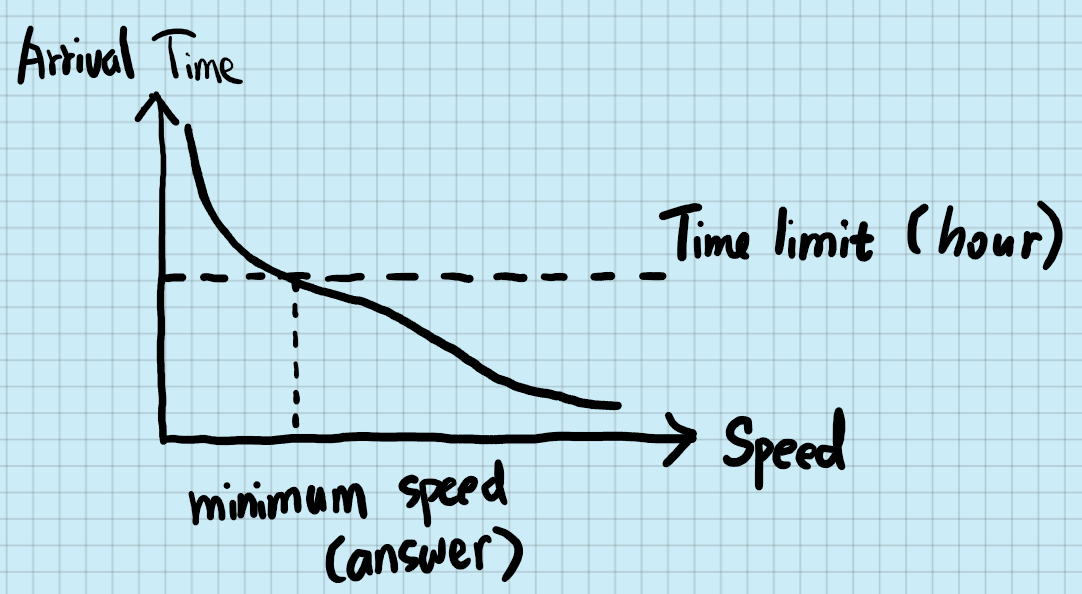
At this point, we can say that this is a binary search problem.

from math import ceil

class Solution:
  def computeArrivalTime(self, dist: List[int], v: int) -> float:
    return sum([ceil(d / v) for d in dist[:-1]] + [dist[-1]/v])
  
  def bSearch(self, dist: List[int], hour: float) -> int:
    lo = 10**-7
    hi = 10**7 + 1
    while lo + 1 < hi:
      mid = (lo + hi) // 2
      if self.computeArrivalTime(dist, mid) <= hour:
        hi = mid
      else:
        lo = mid
    return int(hi)
  
  def minSpeedOnTime(self, dist: List[int], hour: float) -> int:
    if hour <= len(dist) - 1:
      return -1
    return self.bSearch(dist, hour)